How does your car’s GPS find the fastest path to a destination? How does it store the data that enables it to find this path?
These problems led to the creation of a new field in mathematics: graph theory. Data concerning locations and paths connecting those locations can be represented in a graph.
Graphs
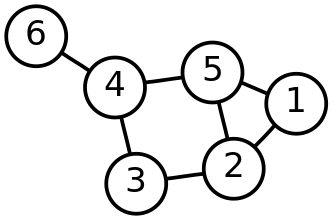
A graph is a collection of vertices and edges, or of nodes and connections. In the above graph, we have six vertices (or nodes) and seven edges (or connections) between the six vertices. For example, one of these edges connects vertices 4 and 6 in the top-left.
|
Note
|
For the purposes of this course, we will mostly refer to vertices and nodes as nodes and edges or connections as edges. |
Graph Theory is the study of graphs, their properties, and their applications.
Properties of Graphs
Graphs have a number of nodes and a number of edges.
Edges may have weights; these commonly denote some sort of cost to "traverse" or distance of an edge. Typically you see these with most applications of graphs.
Graphs can have cycles: a series of distinct edges that lead back to the beginning. In the above example graph, we have the cycles:
\(4\rightarrow 5\rightarrow 2\rightarrow 3\rightarrow 4\),
\(5\rightarrow 1\rightarrow 2\rightarrow 5\),
\(4\rightarrow 5\rightarrow 1\rightarrow 2\rightarrow 3\rightarrow 4\),
and their reverses and rotations. A graph without cycles is acyclic.
So far, we looked at undirected graphs with bidirectional edges, but sometimes edges are directed and can only be traversed in one direction.

Here, we have the cycles:
\(1\rightarrow 2\rightarrow 4\rightarrow 3\rightarrow 1\),
\(1\rightarrow 4\rightarrow 3\rightarrow 1\), and
\(2\rightarrow 4\rightarrow 3\rightarrow 2\).
We can say that two nodes are strongly connected, or adjacent, if the shortest path between them is one edge long. In a directed graph, we say that "a node is adjacent to another node" if the edge leads from the first to the second.
They can be weakly connected, or just connected, if a path exists between them.
Not all graphs are connected, as we’ve seen so far. They can also be disconnected, where you have at least two subgraphs that constitute the larger graph but aren’t connected to each other with an edge.
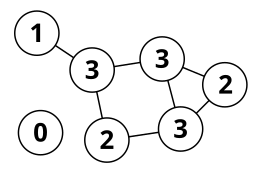
Here, subgraphs \(\{0\}\) and \(\{1,2,2,3,3,3\}\) are internally connected, but not to each other. The graph overall is disconnected.
Trees are connected undirected, acyclic graphs.

These have very interesting properties that will be explored later.
Forests are collections of disconnected trees.
Now that I’ve thrown at you all these terms you have yet to see a use for, it’s time to move on to Implementations and Applications of Graph Theory.
Glossary
- acyclic
-
a graph with no cycles
- adjacent
-
two nodes which are directly connected by a single edge
- connected
-
for a pair of edges \((a,b)\), there is a series of edges which can be traversed from \(a\) to \(b\)
- cycle
-
a series of distinct edges that lead to a loop
- directed edges
-
edges that can only be traversed (or only connects) in one direction
- edge
-
something which connects two edges
- forest
-
a collection of disconnect trees
- graph
-
a collection of nodes and edges
- graph theory
-
the study of graphs
- node
-
an object on which edges can extend from
- tree
-
a connected, undirected, acyclic graph
- unconnected
-
not connected