menu
Subclubs
Artificial Intelligence
Beginners'
All subclubs
Resources
All resources
Options

Minimum Spanning Tree#11

~ / Subclubs / Advanced / Minimum Spanning Tree

Lessons

Previous lesson

Applications of Graph Theory

Next lesson

Shortest Path

Setting Things Up

Introduction to C++

Type Modifiers and Pointers

Standard I/O

Introduction to Algorithms

Recursion and Dynamic Programming Draft

Data Structures Draft

Introduction to Graph Theory Draft

Implementations of Graph Theory Draft

Applications of Graph Theory Draft

Minimum Spanning Tree Draft

Shortest Path Draft

Travelling Salesman

Other Algorithms Draft

This lesson is a draft.

We're currently in the process of finishing this lesson. Check back frequently as we continue to add more content and improve our typos.

an MST

minimum spanning tree

n. a subset of the edges of a connected, edge-weighted graph that connects all nodes together without any cycles and with the minimum possible edge weight; that is, a spanning tree with minimal total weight.

Who cares?

A minimum spanning tree is useful for minimizing costs when connecting nodes in a graph, such as which pipelines to keep in a sewer system during budget cuts.

The idea of a minimum spanning tree can be flipped on its head. Consider a scenario where weights denote restrictions on edges, such as the maximum weight that can be driven across a bridge. Then, to find the maximum weight that can be driven across the network, you just need to find the maximum spanning tree.

Prim’s Algorithm

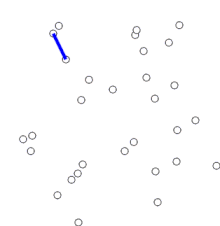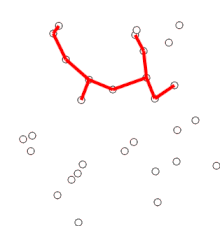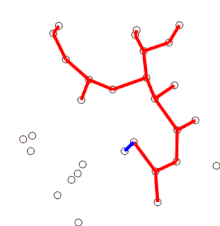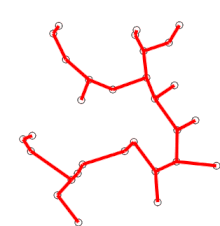
prim’s algorithm on euclidian distance

First developed by Czech mathematician Jarnik in 1930 and later rediscovered and republished by computer scientists Prim and Dijkstra, Prim’s algorithm finds the minimum spanning tree of a graph with \(N\) nodes and \(M\) edges in \(\text{O}(N\log{M})\) time with the tools we have.

Basic Algorithm

  1. Begin with one node[1]. This node is part of your minimum spanning tree.

  2. Iterate until all nodes have been added:

    1. Find the lowest-weight edge that connects from a node currently in the tree to a node not yet in the tree.

    2. Add that edge and the node connected from it to the tree.

Intuition of Correctness

The proof that this works can be understood by induction.

  1. A single node from the graph must, by definition, be a part of the minimum spanning tree.

  2. Adding the least-cost node from the tree to the tree ensures that the two now-connected nodes are connected by the least-weight edge.

Implementation

There are a number of considerations to be had when implementing Prim’s Algorithm.

The following is sample pseudocode:

<span id="L1" class="line"><span class="k">struct</span> <span class="n">less_weight</span> <b class="conum">(1)</b></span>
<span id="L2" class="line"><span class="p">{</span></span>
<span id="L3" class="line">    <span class="kt">bool</span> <span class="k">operator</span><span class="o">&lt;</span><span class="p">(</span><span class="n">edge_t</span> <span class="n">a</span><span class="p">,</span> <span class="n">edge_t</span> <span class="n">b</span><span class="p">)</span></span>
<span id="L4" class="line">    <span class="p">{</span></span>
<span id="L5" class="line">        <span class="c1">//priority_queues are max-heaps, but we want min</span></span>
<span id="L6" class="line">        <span class="k">return</span> <span class="n">a</span><span class="p">.</span><span class="n">weight</span> <span class="o">&gt;</span> <span class="n">b</span><span class="p">.</span><span class="n">weight</span><span class="p">;</span></span>
<span id="L7" class="line">    <span class="p">}</span></span>
<span id="L8" class="line"><span class="p">};</span></span>
<span id="L9" class="line"></span>
<span id="L10" class="line"><span class="n">graph_t</span> <span class="nf">prim</span><span class="p">(</span><span class="n">graph_t</span> <span class="n">g</span><span class="p">)</span></span>
<span id="L11" class="line"><span class="p">{</span></span>
<span id="L12" class="line">    <span class="n">graph_t</span> <span class="n">mst</span><span class="p">;</span></span>
<span id="L13" class="line">    <span class="n">mst</span><span class="p">.</span><span class="n">add_node</span><span class="p">(</span><span class="n">g</span><span class="p">.</span><span class="n">nodes</span><span class="p">[</span><span class="mi">0</span><span class="p">]);</span> <b class="conum">(2)</b></span>
<span id="L14" class="line"></span>
<span id="L15" class="line">    <span class="n">std</span><span class="o">::</span><span class="n">priority_queue</span><span class="o">&lt;</span><span class="n">edge_t</span><span class="p">,</span> <span class="n">std</span><span class="o">::</span><span class="n">vector</span><span class="o">&lt;</span><span class="n">edge_t</span><span class="o">&gt;</span><span class="p">,</span> <span class="n">less_weight</span><span class="o">&gt;</span> <span class="n">choices</span><span class="p">;</span> <b class="conum">(3)</b></span>
<span id="L16" class="line">    <span class="k">for</span> <span class="p">(</span><span class="n">each</span> <span class="n">edge_t</span> <span class="n">e</span> <span class="n">in</span> <span class="n">g</span><span class="p">.</span><span class="n">nodes</span><span class="p">[</span><span class="mi">0</span><span class="p">])</span></span>
<span id="L17" class="line">        <span class="n">choices</span><span class="p">.</span><span class="n">push</span><span class="p">(</span><span class="n">e</span><span class="p">);</span></span>
<span id="L18" class="line"></span>
<span id="L19" class="line">    <span class="k">while</span> <span class="p">(</span><span class="n">mst</span><span class="p">.</span><span class="n">num_nodes</span> <span class="o">&lt;</span> <span class="n">g</span><span class="p">.</span><span class="n">num_nodes</span><span class="p">)</span></span>
<span id="L20" class="line">    <span class="p">{</span></span>
<span id="L21" class="line">    	<span class="k">if</span> <span class="p">(</span><span class="n">mst</span><span class="p">.</span><span class="n">contains_node</span><span class="p">(</span><span class="n">choices</span><span class="p">.</span><span class="n">top</span><span class="p">().</span><span class="n">to_node</span><span class="p">))</span> <b class="conum">(4)</b></span>
<span id="L22" class="line">        <span class="p">{</span></span>
<span id="L23" class="line">            <span class="n">choices</span><span class="p">.</span><span class="n">pop</span><span class="p">();</span></span>
<span id="L24" class="line">            <span class="k">continue</span><span class="p">;</span></span>
<span id="L25" class="line">        <span class="p">}</span></span>
<span id="L26" class="line"></span>
<span id="L27" class="line">        <span class="n">mst</span><span class="p">.</span><span class="n">add_node</span><span class="p">(</span><span class="n">choices</span><span class="p">.</span><span class="n">top</span><span class="p">().</span><span class="n">to_node</span><span class="p">);</span></span>
<span id="L28" class="line">        <span class="n">mst</span><span class="p">.</span><span class="n">add_edge</span><span class="p">(</span><span class="n">choices</span><span class="p">.</span><span class="n">top</span><span class="p">());</span></span>
<span id="L29" class="line"></span>
<span id="L30" class="line">        <span class="n">node_t</span> <span class="n">n</span> <span class="o">=</span> <span class="n">choices</span><span class="p">.</span><span class="n">top</span><span class="p">().</span><span class="n">to_node</span><span class="p">;</span></span>
<span id="L31" class="line">        <span class="n">choices</span><span class="p">.</span><span class="n">pop</span><span class="p">();</span></span>
<span id="L32" class="line"></span>
<span id="L33" class="line">        <span class="k">for</span> <span class="p">(</span><span class="n">each</span> <span class="n">edge_t</span> <span class="n">e</span> <span class="n">in</span> <span class="n">n</span><span class="p">)</span></span>
<span id="L34" class="line">            <span class="n">choices</span><span class="p">.</span><span class="n">push</span><span class="p">(</span><span class="n">e</span><span class="p">);</span></span>
<span id="L35" class="line">    <span class="p">}</span></span>
<span id="L36" class="line"></span>
<span id="L37" class="line">    <span class="k">return</span> <span class="n">mst</span><span class="p">;</span></span>
<span id="L38" class="line"><span class="p">}</span></span>

  1. A functor for STL comparisons

  2. Step 1: add some node to your MST

  3. To carry out step 2a, we’ll keep track of all available choices for the next edge to add in a binary heap. This contributes to the \(\log{M}\) factor in the time complexity.

  4. We do need to consider that an edge may connect two nodes already in the MST. In practice, this is usually accomplished by an array of bools, the \(i\)th element denoting if the \(i\)th node is yet in the MST.

Kruskal’s Algorithm

kruskal’s algorithm on euclidean distance

Developed by American computer scientist Kruskal, and can find the minimum spanning tree of a graph with \(N\) nodes and \(M\) edges in \(\text{O}(M\log{M})\) time, or equivalently, \(\text{O}(M\log{N})\) time.

Basic Algorithm

  1. Sort the \(M\) edges by weight.

  2. Consider each node their own individual tree, forming an \(N\)-node, \(0\)-edge forest, and add them to the MST.

  3. Iterate: take the least-weight not-yet-traversed edge.

    1. If this edge connects two nodes in separate (unconnected) trees, join the two trees together.

Intuition of Correctness

I’m tired, so this is left as an exercise for the reader.

Implementation

Pseudocode:

<span id="L1" class="line"><span class="k">struct</span> <span class="n">less_weight</span> <b class="conum">(1)</b></span>
<span id="L2" class="line"><span class="p">{</span></span>
<span id="L3" class="line">    <span class="kt">bool</span> <span class="k">operator</span><span class="o">&lt;</span><span class="p">(</span><span class="n">edge_t</span> <span class="n">a</span><span class="p">,</span> <span class="n">edge_t</span> <span class="n">b</span><span class="p">)</span></span>
<span id="L4" class="line">    <span class="p">{</span></span>
<span id="L5" class="line">        <span class="c1">//priority_queues are max-heaps, but we want min</span></span>
<span id="L6" class="line">        <span class="k">return</span> <span class="n">a</span><span class="p">.</span><span class="n">weight</span> <span class="o">&gt;</span> <span class="n">b</span><span class="p">.</span><span class="n">weight</span><span class="p">;</span></span>
<span id="L7" class="line">    <span class="p">}</span></span>
<span id="L8" class="line"><span class="p">};</span></span>
<span id="L9" class="line"></span>
<span id="L10" class="line"><span class="n">graph_t</span> <span class="nf">prim</span><span class="p">(</span><span class="n">graph_t</span> <span class="n">g</span><span class="p">)</span></span>
<span id="L11" class="line"><span class="p">{</span></span>
<span id="L12" class="line">    <span class="n">std</span><span class="o">::</span><span class="n">deque</span><span class="o">&lt;</span><span class="n">edge_t</span><span class="o">&gt;</span> <span class="n">all_edges</span> <span class="o">=</span> <span class="n">g</span><span class="p">.</span><span class="n">edges</span><span class="p">;</span> <b class="conum">(1)</b></span>
<span id="L13" class="line">    <span class="n">std</span><span class="o">::</span><span class="n">sort</span><span class="p">(</span><span class="n">all_edges</span><span class="p">.</span><span class="n">begin</span><span class="p">(),</span> <span class="n">all_edges</span><span class="p">.</span><span class="n">end</span><span class="p">(),</span> <span class="n">less_weight</span><span class="p">);</span></span>
<span id="L14" class="line"></span>
<span id="L15" class="line">    <span class="n">graph_t</span> <span class="n">mst</span><span class="p">;</span> <b class="conum">(2)</b></span>
<span id="L16" class="line">    <span class="k">for</span> <span class="p">(</span><span class="n">each</span> <span class="n">node_t</span> <span class="n">n</span> <span class="n">in</span> <span class="n">g</span><span class="p">.</span><span class="n">nodes</span><span class="p">)</span></span>
<span id="L17" class="line">        <span class="n">mst</span><span class="p">.</span><span class="n">add_node</span><span class="p">(</span><span class="n">n</span><span class="p">);</span></span>
<span id="L18" class="line"></span>
<span id="L19" class="line">    <span class="n">dijoint_set_t</span><span class="o">&lt;</span><span class="n">g</span><span class="p">.</span><span class="n">num_nodes</span><span class="o">&gt;</span> <span class="n">connectivity</span><span class="p">;</span> <b class="conum">(3)</b></span>
<span id="L20" class="line"></span>
<span id="L21" class="line">    <span class="k">while</span> <span class="p">(</span><span class="n">connectivity</span><span class="p">.</span><span class="n">num_sets</span> <span class="o">&gt;</span> <span class="mi">1</span><span class="p">)</span></span>
<span id="L22" class="line">    <span class="p">{</span></span>
<span id="L23" class="line">    	<span class="k">if</span> <span class="p">(</span><span class="n">connectivity</span><span class="p">.</span><span class="n">find</span><span class="p">(</span><span class="n">all_edges</span><span class="p">.</span><span class="n">front</span><span class="p">().</span><span class="n">from</span><span class="p">)</span> <span class="o">!=</span></span>
<span id="L24" class="line">            <span class="n">connectivity</span><span class="p">.</span><span class="n">find</span><span class="p">(</span><span class="n">all_edges</span><span class="p">.</span><span class="n">front</span><span class="p">().</span><span class="n">to</span><span class="p">))</span></span>
<span id="L25" class="line">        <span class="p">{</span></span>
<span id="L26" class="line">            <span class="n">connectivity</span><span class="p">.</span><span class="k">union</span><span class="p">(</span><span class="n">all_edges</span><span class="p">.</span><span class="n">front</span><span class="p">().</span><span class="n">from</span><span class="p">,</span> <span class="n">all_edges</span><span class="p">.</span><span class="n">front</span><span class="p">().</span><span class="n">to</span><span class="p">);</span></span>
<span id="L27" class="line">            <span class="n">mst</span><span class="p">.</span><span class="n">add_edge</span><span class="p">(</span><span class="n">all_edges</span><span class="p">.</span><span class="n">front</span><span class="p">());</span></span>
<span id="L28" class="line">        <span class="p">}</span></span>
<span id="L29" class="line">        <span class="n">all_edges</span><span class="p">.</span><span class="n">pop_front</span><span class="p">();</span></span>
<span id="L30" class="line">    <span class="p">}</span></span>
<span id="L31" class="line"></span>
<span id="L32" class="line">    <span class="k">return</span> <span class="n">mst</span><span class="p">;</span></span>
<span id="L33" class="line"><span class="p">}</span></span>

  1. Step 1; I’m using a deque here because there’s less to write later.

  2. Step 2.

  3. It’s very useful to make a disjoint-set structure for checking if two nodes are in the same tree.

Comparison

Prim’s Algorithm Kruskal’s Algorithm

Basis

Node-based

Edge-based

Time Complexity

\(\text{O}(N\log{M})\)

\(\text{O}(M\log{N})\)

Greedy?

Yes

Yes, but less so

Data Structures

Heap

Disjoint-Set

Practice

These are some problems that you can use for practice. The choice of algorithm and modifications are for you to figure out.

CCC03S5: Trucking Troubles

CCC17S4: Minimum Cost Flow

1. any works.