menu
Subclubs
Artificial Intelligence
Beginners'
All subclubs
Resources
All resources
Options

Shortest Path#12

~ / Subclubs / Advanced / Shortest Path

Lessons

Previous lesson

Minimum Spanning Tree

Next lesson

Travelling Salesman

Setting Things Up

Introduction to C++

Type Modifiers and Pointers

Standard I/O

Introduction to Algorithms

Recursion and Dynamic Programming Draft

Data Structures Draft

Introduction to Graph Theory Draft

Implementations of Graph Theory Draft

Applications of Graph Theory Draft

Minimum Spanning Tree Draft

Shortest Path Draft

Travelling Salesman

Other Algorithms Draft

This lesson is a draft.

We're currently in the process of finishing this lesson. Check back frequently as we continue to add more content and improve our typos.

a shortest path

shortest path

n. a subset of the edges of a connected, edge-weighted graph that connects two specific nodes together without any cycles and with the minimum possible total edge weight.

Who cares?

The answer is trivial and is left as an exercise to the reader[1].

Relaxing an Edge

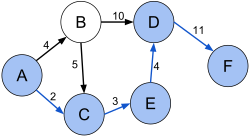
a shortest path

Consider the graph on the right, where we are searching for a path from node A to node F.

The true distance to node A is \(0\), as the total weight of the shortest path from A to A is \(0\). Similarly, the true distance to node B is \(4\), to node C is \(2\), etc.

This is because the shortest path to B is \(A\rightarrow B\) with weight \(4\), and the shortest path the C is \(A\rightarrow C\) with weight \(2\); the only other path is \(A\rightarrow B\rightarrow C\) with weight \(4+5=9\).

To find, then, the distance to node D, we must consider three paths:

\(A\rightarrow B\rightarrow D\) with weight \(4+10=14\),

\(A\rightarrow B\rightarrow C\rightarrow E\rightarrow D\), with weight \(4+5+3+4=16\), and

\(A\rightarrow C\rightarrow E\rightarrow D\), with weight \(2+3+4=9\).

Since the third path has least weight, the true distance from node A to node D is \(9\).

Notice that we could have found this if we already knew the true distance from node A to nodes B or E: we could take that distance and add the weight of edges \(B\rightarrow D\) or \(E\rightarrow D\) respectively.

The act of doing so is called relaxing an edge: finding (and updating) the true distance of some node Y from edge \(X\rightarrow Y\).

Dijkstra’s Algorithm

dijkstra’s algorithm on euclidean distance

Developed by Edsger W. Dijkstra, Dijkstra’s Algorithm finds the shortest path between two nodes in a nonnegative-weighted graph with \(N\) nodes and \(M\) edges in \(\Theta(M\log{M})\) time using a binary heap.

Basic Algorithm

  1. Begin with true distance \(\infty\) for all nodes.

  2. Add the source node to the open list with true distance \(0\).

  3. Until there are no more open nodes, or until the destination node is marked closed, iterate:

    1. Pick the least true-distance open node.

    2. Relax all edges from this node.

    3. Close this node.

Intuition of Correctness

This is equivalent to what would be breadth-first search if, instead of merely considering recursive depth, the true distance of a node were considered instead. As such, every node closed must be the next-closest open node to the source.

Implementation

<span id="L1" class="line"><span class="k">struct</span> <span class="n">less_true_dist</span> <b class="conum">(1)</b></span>
<span id="L2" class="line"><span class="p">{</span></span>
<span id="L3" class="line">    <span class="kt">bool</span> <span class="k">operator</span><span class="o">&lt;</span><span class="p">(</span><span class="n">edge_t</span> <span class="n">a</span><span class="p">,</span> <span class="n">edge_t</span> <span class="n">b</span><span class="p">)</span></span>
<span id="L4" class="line">    <span class="p">{</span></span>
<span id="L5" class="line">        <span class="c1">//priority_queues are max-heaps, but we want min</span></span>
<span id="L6" class="line">        <span class="k">return</span> <span class="n">a</span><span class="p">.</span><span class="n">to</span><span class="p">.</span><span class="n">true_dist</span> <span class="o">&gt;</span> <span class="n">b</span><span class="p">.</span><span class="n">to</span><span class="p">.</span><span class="n">true_dist</span><span class="p">;</span></span>
<span id="L7" class="line">    <span class="p">}</span></span>
<span id="L8" class="line"><span class="p">};</span></span>
<span id="L9" class="line"></span>
<span id="L10" class="line"><span class="kt">int</span> <span class="nf">dijkstra</span><span class="p">(</span><span class="n">graph_t</span> <span class="n">g</span><span class="p">,</span> <span class="n">node_t</span> <span class="n">source</span><span class="p">,</span> <span class="n">node_t</span> <span class="n">dest</span><span class="p">)</span></span>
<span id="L11" class="line"><span class="p">{</span></span>
<span id="L12" class="line">    <span class="n">g</span><span class="p">.</span><span class="n">set_all_true_dist</span><span class="p">(</span><span class="n">MAXINT</span><span class="p">);</span> <b class="conum">(2)</b></span>
<span id="L13" class="line"></span>
<span id="L14" class="line">    <span class="n">std</span><span class="o">::</span><span class="n">priority_queue</span><span class="o">&lt;</span><span class="n">edge_t</span><span class="p">,</span> <span class="n">std</span><span class="o">::</span><span class="n">vector</span><span class="o">&lt;</span><span class="n">edge_t</span><span class="o">&gt;</span><span class="p">,</span> <span class="n">less_true_dist</span><span class="o">&gt;</span> <span class="n">open_list</span><span class="p">;</span></span>
<span id="L15" class="line">    <span class="n">open_list</span><span class="p">.</span><span class="n">push</span><span class="p">(</span><span class="n">make_edge</span><span class="p">(</span><span class="nb">NULL</span><span class="p">,</span> <span class="n">source</span><span class="p">,</span> <span class="mi">0</span><span class="p">,</span> <span class="mi">0</span><span class="p">));</span> <b class="conum">(3)</b></span>
<span id="L16" class="line"></span>
<span id="L17" class="line">    <span class="k">while</span> <span class="p">(</span><span class="o">!</span><span class="n">dest</span><span class="p">.</span><span class="n">closed</span><span class="p">()</span> <span class="o">&amp;&amp;</span> <span class="o">!</span><span class="n">open_list</span><span class="p">.</span><span class="n">empty</span><span class="p">())</span></span>
<span id="L18" class="line">    <span class="p">{</span></span>
<span id="L19" class="line">    	<span class="n">edge_t</span> <span class="n">next</span> <span class="o">=</span> <span class="n">open_list</span><span class="p">.</span><span class="n">top</span><span class="p">();</span></span>
<span id="L20" class="line">        <span class="n">open_list</span><span class="p">.</span><span class="n">pop</span><span class="p">();</span></span>
<span id="L21" class="line">        <span class="k">if</span> <span class="p">(</span><span class="n">next</span><span class="p">.</span><span class="n">to</span><span class="p">.</span><span class="n">closed</span><span class="p">())</span></span>
<span id="L22" class="line">            <span class="k">continue</span><span class="p">;</span></span>
<span id="L23" class="line"></span>
<span id="L24" class="line">        <span class="n">next</span><span class="p">.</span><span class="n">close</span><span class="p">();</span> <b class="conum">(4)</b></span>
<span id="L25" class="line">        <span class="k">for</span> <span class="p">(</span><span class="n">each</span> <span class="n">edge_t</span> <span class="n">e</span> <span class="n">in</span> <span class="n">next</span><span class="p">.</span><span class="n">to</span><span class="p">.</span><span class="n">edges</span><span class="p">)</span></span>
<span id="L26" class="line">        <span class="p">{</span></span>
<span id="L27" class="line">            <span class="k">if</span> <span class="p">(</span><span class="o">!</span><span class="n">e</span><span class="p">.</span><span class="n">to</span><span class="p">.</span><span class="n">closed</span><span class="p">()</span> <span class="o">&amp;&amp;</span> <span class="n">relax</span><span class="p">(</span><span class="n">e</span><span class="p">))</span> <b class="conum">(5)</b></span>
<span id="L28" class="line">            <span class="p">{</span></span>
<span id="L29" class="line">            	<span class="n">open_list</span><span class="p">.</span><span class="n">push</span><span class="p">(</span><span class="n">e</span><span class="p">);</span></span>
<span id="L30" class="line">            <span class="p">}</span></span>
<span id="L31" class="line">        <span class="p">}</span></span>
<span id="L32" class="line">    <span class="p">}</span></span>
<span id="L33" class="line"></span>
<span id="L34" class="line">    <span class="k">return</span> <span class="n">dest</span><span class="p">.</span><span class="n">true_dist</span><span class="p">;</span></span>
<span id="L35" class="line"><span class="p">}</span></span>

  1. A functor for STL comparisons

  2. Step 1. Usually you’d store these in an array.

  3. Step 2. Assume that make_edge has signature edge_t make_edge(node_t from, node_t to, int weight, int true_dist) and parameters are passed by reference.

  4. Assume that this closes the node next.to, automatically updating true distance.

  5. relax(edge_t e) updates node e.to with its true distance, if applicable, and returns true on an update; that is, a new least true distance was found.

Bellman-Ford Algorithm

First proposed by Alfonso Shimbell in 1955 and later named after mathematicians Richard Bellman and Lester Ford Jr. who published it, the Bellman-Ford algorithm can find the shortest path in a graph with negative weights or report the existence of a negative cycle in a graph with \(N\) nodes and \(M\) edges in \(\text{O}(NM)\) time.

Basic Algorithm

  1. Begin with true distance \(\infty\) for all nodes except the source, which starts with true distance \(0\).

  2. Relax all \(M\) edges \(N\) times.

    1. If any relaxing on the \(N^{\text{th}}\) pass succeeded, a negative cycle was found.

Intuition of Correctness

This is pretty much brute-force.

Implementation

<span id="L1" class="line">int bellman_ford(graph_t g, node_t source, node_t dest)</span>
<span id="L2" class="line">{</span>
<span id="L3" class="line">    g.set_all_true_dist(MAX_INT); <b class="conum">(1)</b></span>
<span id="L4" class="line">    source.set_true_dist(0);</span>
<span id="L5" class="line"></span>
<span id="L6" class="line">    bool successful_relax = false;</span>
<span id="L7" class="line">    for (int n = 0; n &lt; g.num_nodes; ++n)</span>
<span id="L8" class="line">    {</span>
<span id="L9" class="line">        successful_relax = false; <b class="conum">(2)</b></span>
<span id="L10" class="line">        for (each edge_t e in g.edges)</span>
<span id="L11" class="line">        {</span>
<span id="L12" class="line">            successful_relax = successful_relax | relax(e); <b class="conum">(3)</b></span>
<span id="L13" class="line">        }</span>
<span id="L14" class="line">        if (!successful_relax)</span>
<span id="L15" class="line">            break;</span>
<span id="L16" class="line">    }</span>
<span id="L17" class="line"></span>
<span id="L18" class="line">    if (successful_relax) <b class="conum">(4)</b></span>
<span id="L19" class="line">        return -1;</span>
<span id="L20" class="line"></span>
<span id="L21" class="line">    return dest.true_dist;</span>
<span id="L22" class="line">}</span>

  1. Step 1.

  2. This is to track if any relaxing was successful; if there wasn’t, there’s no need to continue.

  3. This is a quick hack for something that’s equivalent to if(relax(e)) relax = true; in less statements. The single-bar isn’t an error: a double-bar would short circuit if successful_relax were already true, skipping the actual relaxing.

  4. If the last iteration contained a successful relax, then there’s a negative cycle, in which case we return an error code. In this case, it’s -1.

Comparison

Dijkstra’s Algorithm Bellman-Ford Algorithm

Basis

Node-based

Edge-based

Time Complexity

\(\Theta(M\log{M})\)

\(\text{O}(NM)\)

Greedy?

Yes — no negative weights

No

Data Structures

Heap

No

Practice

These are some problems that you can use for practice. The choice of algorithm and modifications are for you to figure out.

GRAPH3P2: Shortest Path

PIPE: Pipe Dream

CCC15S4: Convex Hull

CCC08S3: Maze

MockCCC14S4: Roadtrip Tracking

1. pathfinding, duh