Sections

• Loops
• Strings
• Arrays

These questions are here to test and reinforce your understanding of key concepts so that you can ease into doing contest questions.

Loops

1. Write a program that outputs a smiley face, :), an n number of times.

   Input: n (integer)

   Output: ":)" written n times

   Sample Run

   Input	Output
   2	:):)
   7	:):):):):):):)

2. Write a program that outputs the first 5 multiples of n.

   Input: n (integer)

   Output: the first 5 multiples of n, starting with n

   Sample Run

   Input	Output
   1	1 2 3 4 5
   17	17 34 51 68 85
   -8	-8 -16 -24 -32 -40

3. Write a program that takes integers n and i. Your program will perform i calculations on n. The calculations done on n will alternate between the following:

   1. \(n_{\text{next}} = 2(n + 4)\)

   2. \(n_{\text{next}} = \dfrac{n + 2}{2}\)

   The program will output the final value of n.

   Input: n i

   Output: resulting number after performing i calculations to n

   Sample Input: \(\textcolor{red}{3}, 5\)

   Sample Output: 34

   Explanation:

   \[\begin{aligned} 2(\textcolor{red}{3}+4) &= \textcolor{blue}{14} \\ \frac{\textcolor{blue}{14}+2}{2} &= \textcolor{orange}{8} \\ 2(\textcolor{orange}{8}+4) &= \textcolor{green}{24} \\ \frac{\textcolor{green}{24}+2}{2} &= \textcolor{purple}{13} \\ 2(\textcolor{purple}{13}+4) &= \boxed{34} \end{aligned}\]

   Sample Run

   Input	Output
   9 4	19
   -12 9	24
   35 16	75
   1071 13789	71090

4. Suppose a number of dots were used to form an equilateral triangle. The number of dots required to make the triangle increases as the number of rows increases. Notice how the number of dots in each row increases by one each time.

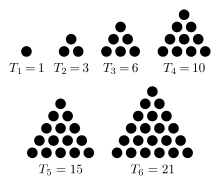
   1. Given an n number of rows, determine the number of dots needed to make an equilateral triangle.

      Input: \(n, n>0\)

      Output: the number of dots required to make the triangle

      Sample Run

      Input	Output
      6	21
      12	78
      256	32896

   2. The number of dots that form an equilateral triangle are called triangular numbers. In a sequence of all triangular numbers, t(n), t(n) would be the sum of all natural numbers up to and including n; that is, \(t(n) = 1 + 2 + 3 + \cdots + n\)

      There is a formula that calculates the \(n^{th}\) term in a sequence of triangle numbers:

      \[t(n) = \frac{n(n + 1)}{2}\]

      Rewrite your program so that it now uses this formula to calculate the number of dots in an equilateral triangle. If you have originally used this method, then rewrite your program so that it uses loops instead. Use the same test data as [4(a)].

5. The Fibonacci sequence is a list of numbers where each term is the sum of the previous two terms.

   \[F_{n} = F_{n - 1} + F_{n - 2}\]

   Let the zeroth and first term of the Fibonacci sequence be 0 and 1, respectively. Write a program that outputs the \(n^{th}\) term of the fibonacci sequence.

   Input: \(n\)

   Output: \(n^{th}\) term of the Fibonacci sequence

   Sample Run

   Input	Output
   5	5
   13	233
   33	3524578

   Hint (Highlight to see): To find the \(n^{th}\) term in the sequence, you will start with the zeroth and first term and find all succeeding terms until you get to the \(n^{th}\) term.

6. The 3n+1 problem. The wcipeg page explains this nicely.

   Hint (Highlight to see): The number of times 3n+1 and n/2 will be calculated is unknown. A while loop would suit this question.

Strings

1. 1. Write a program that takes a word and outputs the reverse of a word.

      Sample Run

      Input	Output
      abbc	cbba
      qwertyuiop	poiuytrewq

   2. A palindrome is a string that can be read the same backward and forward. Write a program that takes a word and determines if it is a palindrome. If it is a palindrome, output YES. If it is not a palindrome, output NO.

      Sample Run

      Input	Output
      abcddcba	YES
      a	YES
      qwertyqwerty	NO

2. Write a program that takes a word. Going through the index (\(i\)) of every character, output the \(i^{th}\) character in the word \(i+1\) times.

   Sample Run

   Input	Output
   abc	abbccc
   qwerty	qwweeerrrrtttttyyyyyy
   booo	booooooooo

3. 1. Write a program that takes a word, then a character c. Your program will determine the number of times the character is found in the word.

      Sample Run

      Input	Output
      mississippi s	4
      lolloooolooolasdoo o	10
      kappa o	0

   2. Modify the program so that it will remove all instances where c appears in the word.

      You may want to use string::erase from the string library.

      Sample Run

      Input	Output
      mississippi s	miiippi
      lolloooolooolasdoo o	lllllasd
      kappa o	kappa

   3. Modify your program again so that it accepts two characters this time, c1 and c2. Each time c1 is found in the string, the character is replaced with c2 instead. Each time c2 is found in the string, the character is replaced with c1.

      Sample Run

      Input	Output
      mississippi i s	msiisiispps
      lolloooolooolasdoo o l	oloollllollloasdll
      kappa p p	kappa

4. 1. Write a program that will take a character. If the character is an uppercase letter, output "U". If the character is a lowercase letter, output "L". If the character is not a letter, output "N".

      Sample Run

      Input	Output
      S	U
      t	L
      @	N

   2. Write a program that will take a word, and output the word in all caps. I suggest you refer to an ASCII table instead of 26 if statements.

      Sample Run

      Input	Output
      Hello	HELLO
      l33t	L33T
      HoWiSLife??3	HOWISLIFE??3

5. Write a program that takes an entire line of characters. You will need to use the getline() function. After receiving an entire sentence, output the sentence with all the words reversed. Assume no punctuation will be given in the input.

   Sample Run

   Input	Output
   The cake is a lie	lie a is cake The
   Whotypeswithspacesanyways	Whotypeswithspacesanyways
   All the words in the sentence must be reversed	reversed be must sentence the in words the All

   Hint (Highlight to see): All words are surrounded by spaces, and spaces are also characters. The length of each word in a sentence can be found be locating all the spaces in the sentence.

6. Hidden Palindrome is a good contest question that you can find on WCIPEG. (Ex: In the string abcba, bcb is a palindrome surrounded by two a’s)

   Hint 1 (Highlight to see): A palindrome is made up of a smaller palindrome surrounded by two of the same characters.

   Hint 2 (Highlight to see): A way to check if a string is a palindrome is to start at the centre of the string and work outwards. For example, suppose i is the index of the centre of the string. For the string to be a palindrome, str[i-n] and str[i+n] must be the same. This idea should be used when finding hidden palindromes.

   The solution to Hidden Palindrome can be found in the here.

Arrays

1. Write a program that takes in an n number of integer inputs. This program will store those integers in an array and determine the greatest number (h) and least number (l) of all the given integers.

   Input: \(n\); \(k_1\) to \(k_n\), the number of integers which follow \(n\) integers

   Output: h l

   Sample Run

   Input	Output
   7 1 2 0 3 8 4 9	9 0
   16 11 2 93 82 78 54 1 82 -90 2 8 3 4 5 1 -3	93 -90

2. Write a program that takes an n number of integers. Store all the integers into an array. Reorder the elements in the array so that all the values in the array are reversed. Do not make a copy of the array while reversing. After reversing, output the \(i^{th}\) element of the reversed array. i will always be less than n.

   Input: \(n\); \(k_1\) to \(k_n\), the number of integers which follow \(n\) integers
   \(i\), \(0 \le i < n\)

   Output: The value of the element in the reversed array at index i.

   Sample Run

   Input	Output
   10 2 4 6 8 10 12 14 16 18 20 6	8
   5 1 2 3 4 5 1	4

3. 1. Write a program that takes n integers from 0 to 9. Determine the number of times i appears in the array.

      Input: *n*, the number of integers which follow n integers, k₀ to k_n-1
      *i*, the integer to count

      Output: The number of times i appeared as an input.

      Sample Run

      Input	Output
      6 5 9 8 3 3 2 3 3	3
      20 1 0 1 1 1 1 1 0 1 1 1 0 1 1 1 0 1 1 0 1 1	15

   2. Write a program that will continually accept integer inputs from 0-9 until it receives a -1. Determine the number of times i appears in the array.

      Input: An unknown amount of integers from 0-9 , terminated by -1
      *i*, the integer to count

      Output: The number of times i appeared as an input.

      Sample Run

      Input	Output
      1 6 3 2 4 1 1 2 3 5 1 5 3 7 2 4 3 7 1 3 2 -1 1	5
      7 4 9 8 4 5 2 6 7 4 3 4 -1 4	4

      Hint (Highlight to see): Instead of having an array that stores all integer inputs, have an array that stores the number of times each number has been inputted so far.

4. 1. An anagram is a rearrangement of the letters of a word/phrase to form another word/phrase. Write a program that will determines if two phrases are anagrams. You will need to use getline() for this question. If the two phrases are anagrams, output “Y”. If the two phrases are not anagrams, output “N”.

      Sample Run

      Input	Output
      dormitory dirty room	Y
      eleven plus two twelve plus one	Y
      abracadabra cabra darab	N

      Hint (Highlight to see): have a 26 element array that stores how many times each character appears in a string.

   2. Ragaman is a variation of the problem above. This question can be found on the WCIPEG website.

      Hint (Highlight to see): Since the first word will never have any asterisks, if the second word has more of one character than the first word, the two words are not ragamans.

   3. Eliminanagram is another problem that involves anagrams. This can also be found on the WCIPEG site.

      Hint (Highlight to see): For two words to be eliminanagrams, the total number of each character found in the two words must be even.